ここでは、探索的因子分析で尺度項目の候補として残った42項目について、6つの上位概念それぞれに測定方程式をたてて分析を進める。測定方程式とは、共通の原因としての潜在変数が複数個の観測変数に影響を与えている様子を記述するための方程式で、影響力の指標である因果係数を推定することは共分散構造分析の目的の1つである。
分析結果を評価するときに、最初に参照すべき指標は、「GFI;適合度指標」と呼ばれる統計量である。GFIは、通常は0〜1までの値をとり、その値が1に近いモデルほど、説明力のあるモデルと判断する。しかし、統計モデルでは、母数の数を増やして複雑なモデルを構成すると、モデルの見せかけ上の説明力が上昇するという傾向があり、複雑なモデルは、単純なモデルと比較して母数の推定値の「安定性」が悪くなる。そのため複雑なモデルでは、その説明力から不安定度を割り引きして示す指標として、「AGFI」がある。AGFIも1に近いほどデータへの当てはまりが良いモデルであると判断すればよい。また、GFIとAGFIの間には、GFI≧AGFIという関係があり、GFIにくらべてAGFIが著しく低下する場合は、あまり好ましいモデルとは言えない。
GFIやAGFIは、モデルがデータを説明する割合を示し、分かりやすい解釈を与える指標であるのに対して、複数のモデルを比較する際の、モデルの相対的な良さを評価するための指標であるのが、AIC(Akaike’s Information Criterion)である。AICは、値が小さいほどモデルのデータに対する当てはまりがよいと解釈されるため、いくつかのモデルが候補にあがった場合、その中からAICの値の最も小さいものを最適のモデルとして選択すればよい。
設定した因果モデルが、結果となる潜在変数や観測変数を十分に因果的に規定していることを確認するためには、結果となる変数の変動が、モデルに導入された誤差以外の変数によって説明される割合が高いことが必要である。それの検討のためには、R-spuared(決定係数)と呼ばれる指標を吟味すればよい。決定係数は、モデル内部の「構造的な変数」が「内生変数」を説明する割合を示す指標で、その値は設定した因果連鎖が有効なものか否かを判断する材料となるため、この値が余りにも小さいモデルは、原因としてモデルに導入した構造変数では結果変数の変動が予測できないことになる。
以上の数値に注目して分析していくのだが、まずは潜在変数から観測変数への影響指標を概念別に見ていきたい。
以下は、各概念ごとの分析結果である。

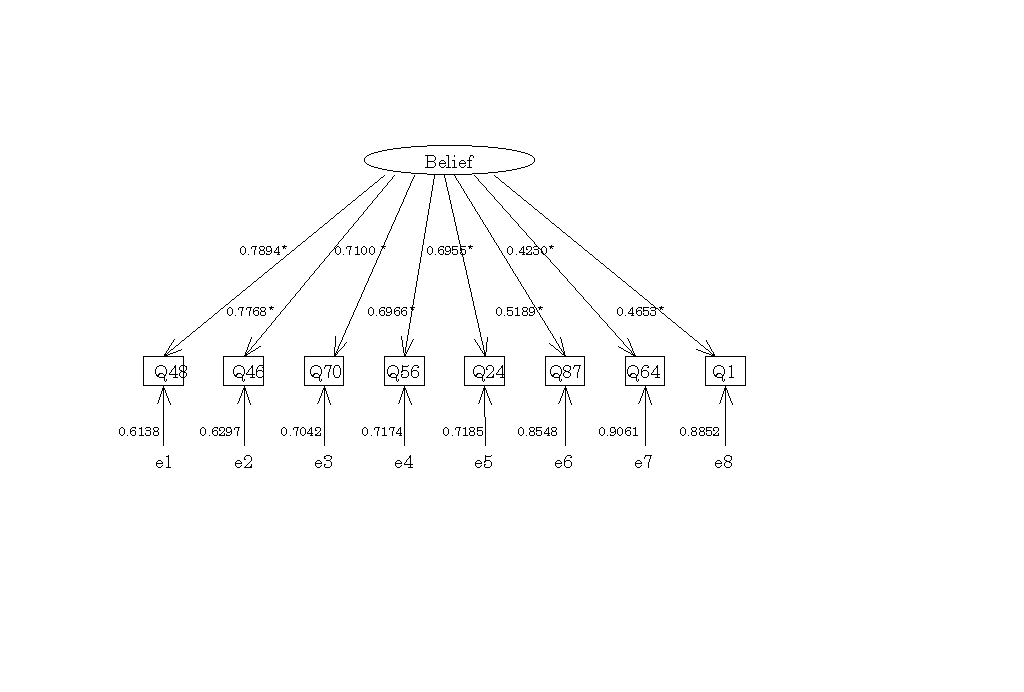
図7 Beliefの概念内のパス図
表10-1Beliefの概念に対する適合度指標
|
GFI |
AGFI |
適合度χ二乗 |
自由度 |
危険度 |
AIC |
HoelterのN |
| .9519 | .9088 | 23.6208 | 19 | .2111 | -14.3792 | 153 |
表10
-2 決定係数|
Q48 |
Q46 | Q70 | Q56 | Q24 | Q87 |
Q64 |
Q1 |
| .623218 | .603488 | .504129 | .485283 | .483705 | .269250 | .178957 | .216492 |
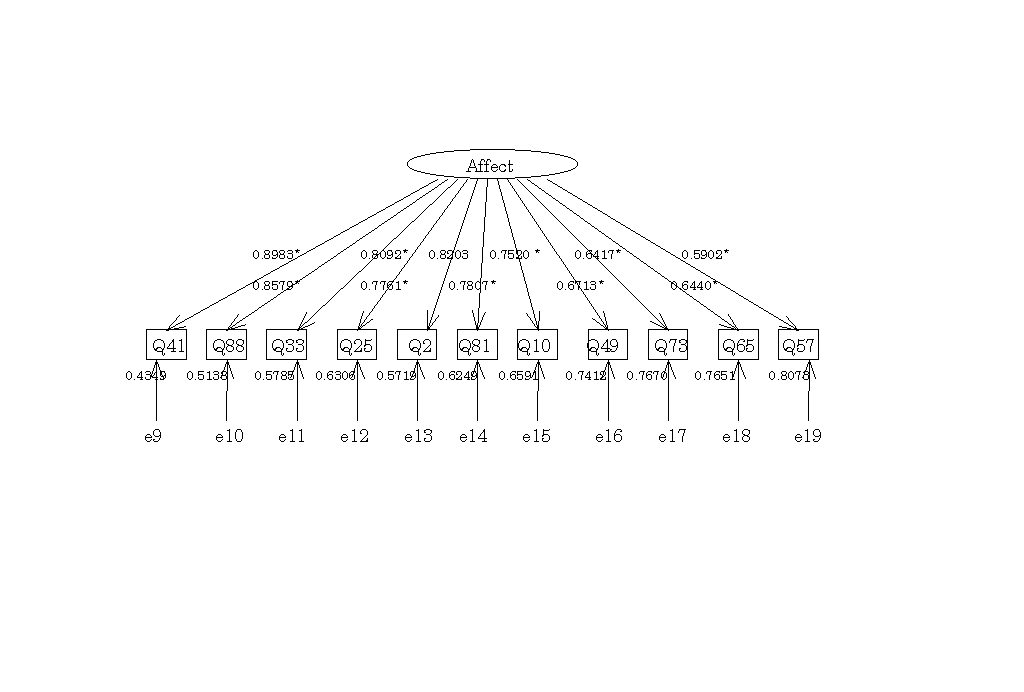
図8
Affectの概念内のパス図
表11
-1 Affectの概念に対する適合度指標|
GFI |
AGFI |
適合度χ二乗 |
自由度 |
危険度 |
AIC |
HoelterのN |
| .8644 | .7919 | 108.2259 | 43 | .0001 | 22.2259 | 67 |
表11
-2 決定係数|
Q41 |
Q88 | Q33 | Q25 | Q2 | Q81 | Q10 | Q49 | Q73 | Q65 |
Q57 |
| .806961 | .736009 | .654824 | .602306 | .672913 | .609474 | .565599 | .450607 | .411783 | .414697 | .348338 |
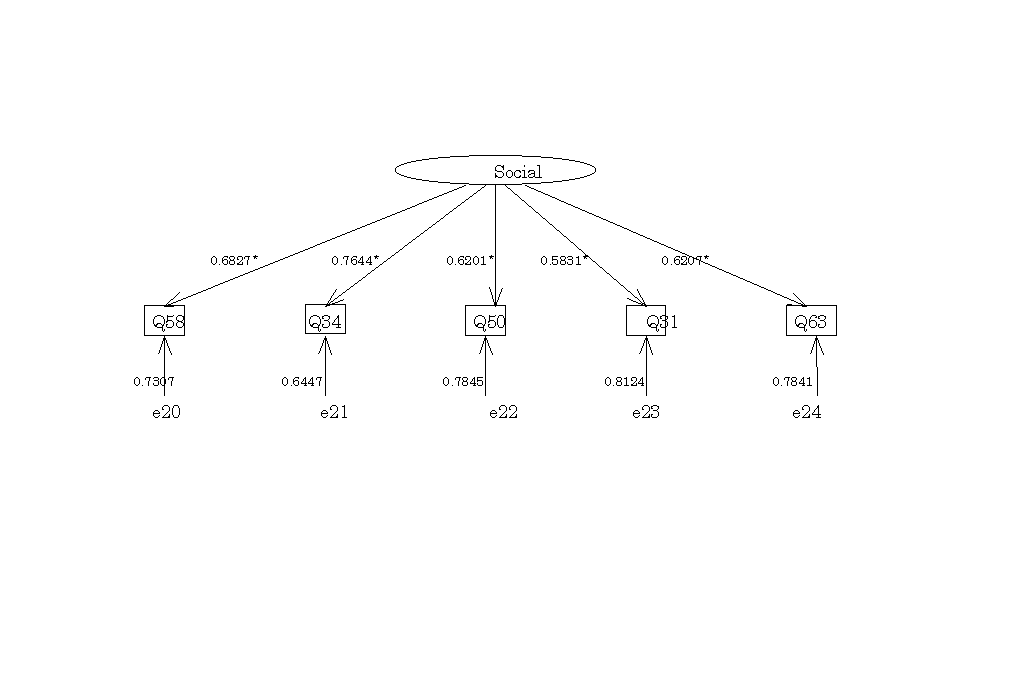
図9
Socialの概念内のパス図
表12
-1 Socialの概念に対する適合度指標|
GFI |
AGFI |
適合度χ二乗 |
自由度 |
危険度 |
AIC |
HoelterのN |
| .9735 | .9008 | 7.4522 | 4 | .1138 | -0.5478 | 153 |
表12
-2 決定係数|
Q58 |
Q34 |
Q50 |
Q31 |
Q63 |
| .466129 | .584350 | .384519 | .340044 | .385214 |
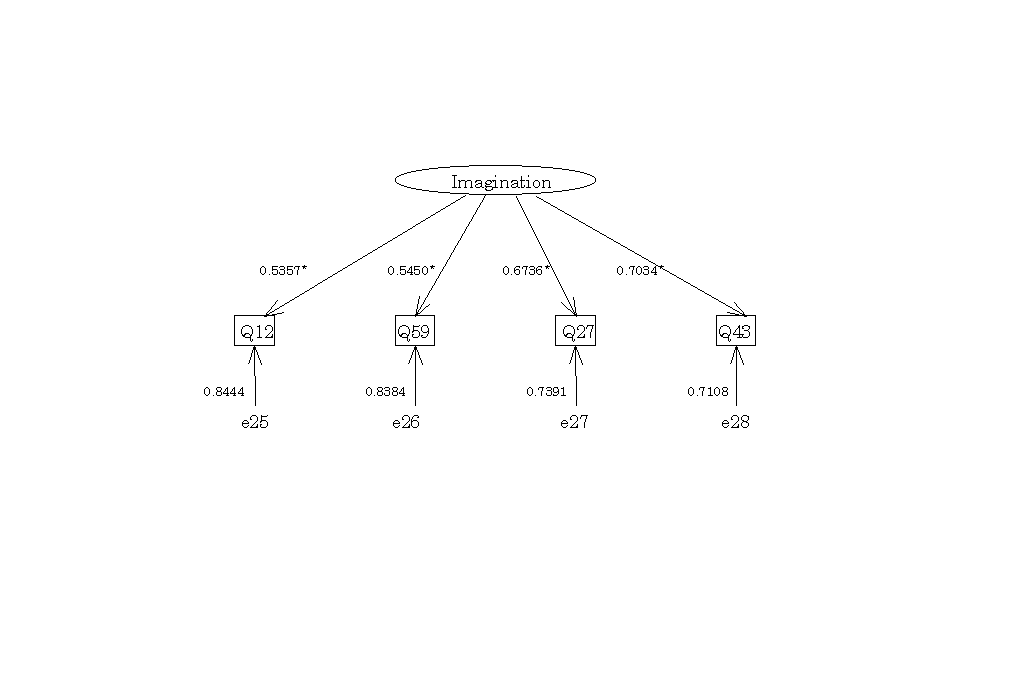
図10
Imaginationの概念内のパス図表13
-1 Imaginationの概念に対する適合度指標|
GFI |
AGFI |
適合度χ二乗 |
自由度 |
危険度 |
AIC |
HoelterのN |
| .9822 | .8221 | 4.2963 | 1 | .0382 | 2.2963 | 108 |
表13
-2 決定係数|
Q12 |
Q59 |
Q27 |
Q43 |
| .286993 | .297076 | .453693 | .494777 |
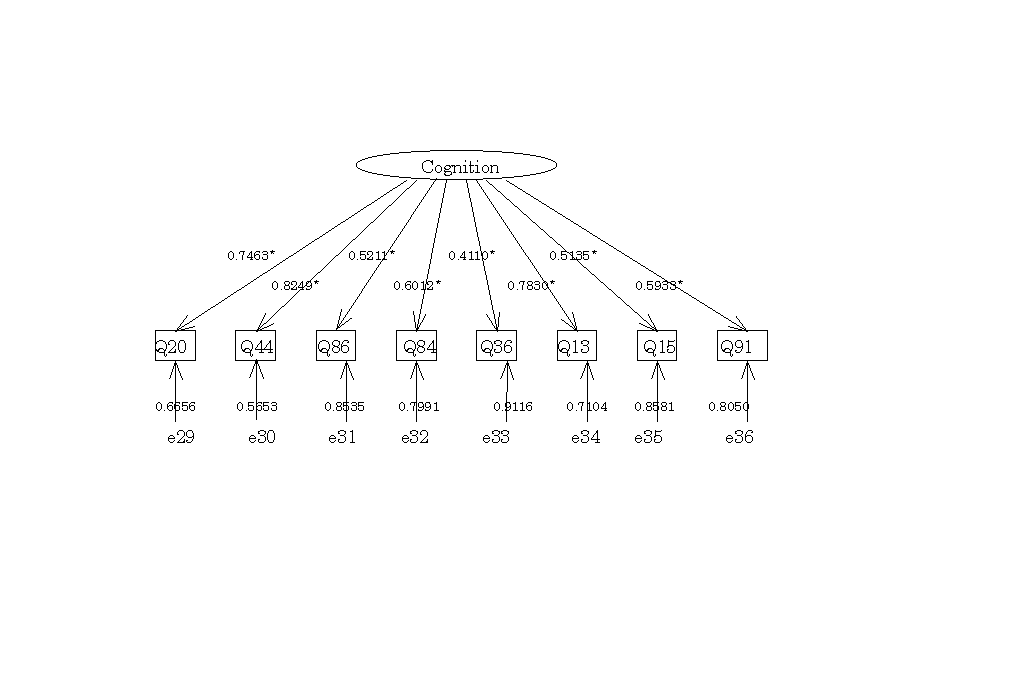
図11
Cognitionの概念内のパス図表14
-1 Cognitionの概念に対する適合度指標|
GFI |
AGFI |
適合度χ二乗 |
自由度 |
危険度 |
AIC |
HoelterのN |
| .9189 | .8464 | 41.7521 | 19 | .0019 | 3.7521 | 87 |
表14
-2 決定係数|
Q20 |
Q44 | Q86 | Q84 | Q36 | Q13 | Q15 |
Q91 |
| .556944 | .680422 | .271591 | .361408 | .168913 | .495314 | .263659 | .352046 |
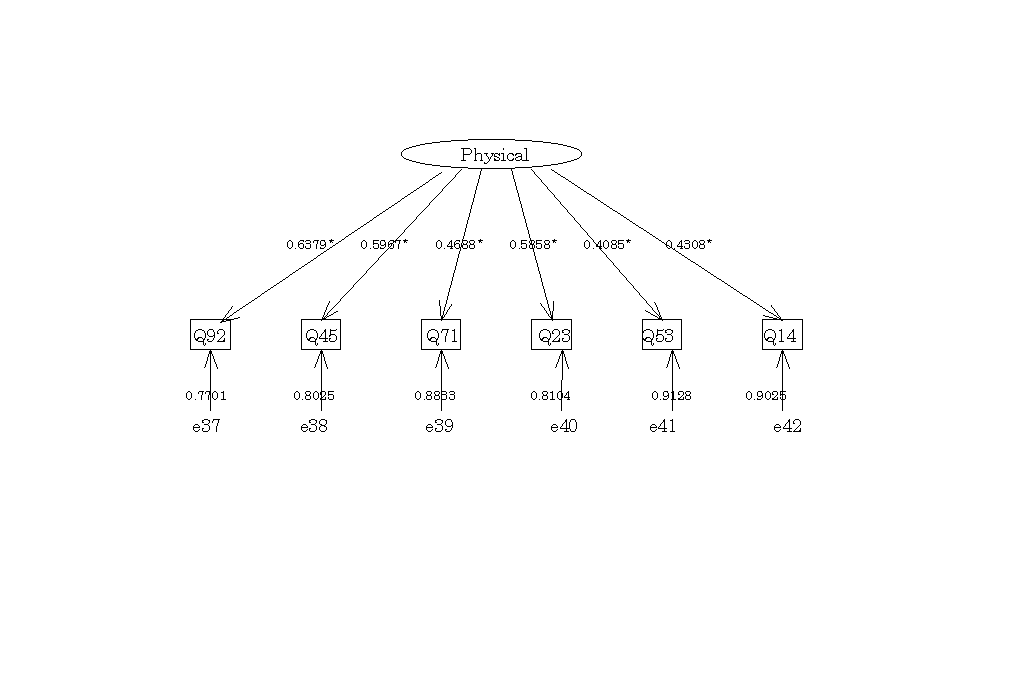
図12
Physicalの概念内のパス図表15
-1 Physicalの概念に対する適合度の指標|
GFI |
AGFI |
適合度χ二乗 |
自由度 |
危険度 |
AIC |
HoelterのN |
| .9555 | .8832 | 15.4513 | 8 | .0509 | -0.5487 | 121 |
表15
-2 決定係数|
Q92 |
Q45 |
Q71 |
Q23 |
Q53 |
Q14 |
| .406873 | .355997 | .219799 | .343186 | .166837 | .185562 |