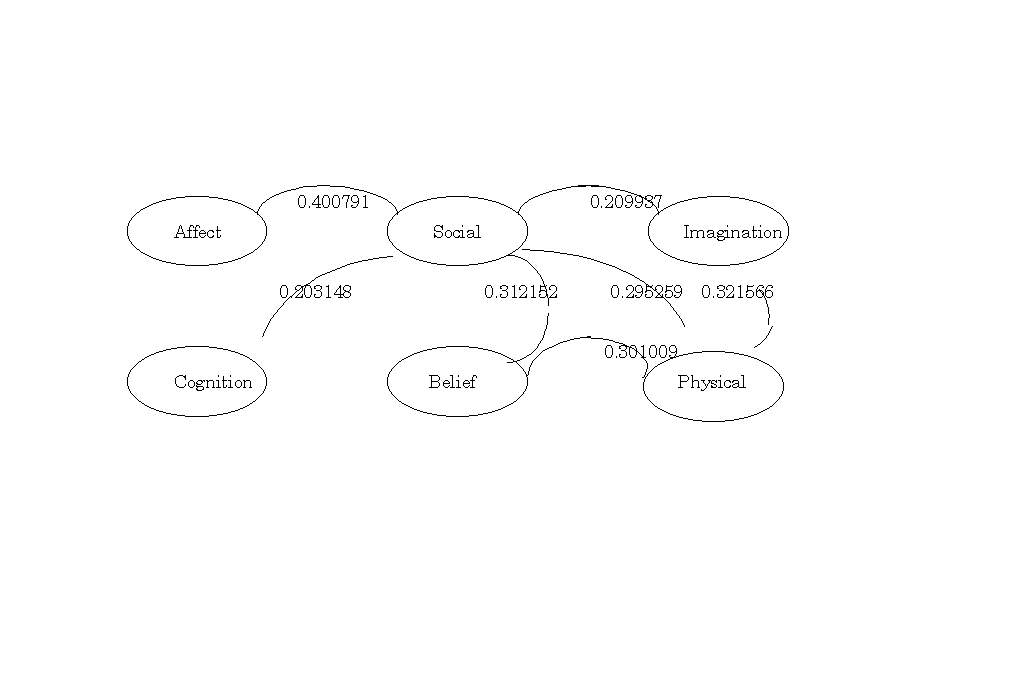
次に、全ての概念を組み込んで、どの概念間で相関があるのかを調べた。相関関係の強さについては、一般に相関係数の絶対値が
0.2以下であれば「ほとんど相関がない」、0.2〜0.4くらいであれば「弱い相関がある」、0.4〜0.7くらいであれば「強い相関がある」、と表現されることが多い。ここでは、相関値0.2以上のものを有意であると判断した。その結果、BeliefとSocialの間で0.312152、BeliefとPhysicalの間で0.301009、AffectとSocialの間で0.400791、ImaginationとSocialの間で0.209937、ImaginationとPhysicalの間で0.321566、CognitionとSocialの間で0.203148、PhysicalとSocialの間で0.295259の相関が認められた(図13)。

図13 概念間の相関を表したパス図
ここで、上記のようなモデルを構成できたのであるが、データを手にして最初に構成したモデルが、そのデータにとって必ずしも最適なモデルであるとは限らない。一般に、最終的なモデルを絞り込むまでには、1つのデータに対して複数のモデルを構成し、その結果を比較・評価することが必要である。そこで、モデルの全体的評価と部分的評価を行い、モデルを改良しデータの再分析を行うことにする。
最初に構成したモデルが最も妥当であると仮定して、上記の分析の結果を利用し、他にも複数のモデルを構成して、その結果を比較・評価してみた。その結果、図13のモデルよりも、有意な数値のモデルを得ることができた(図14)。
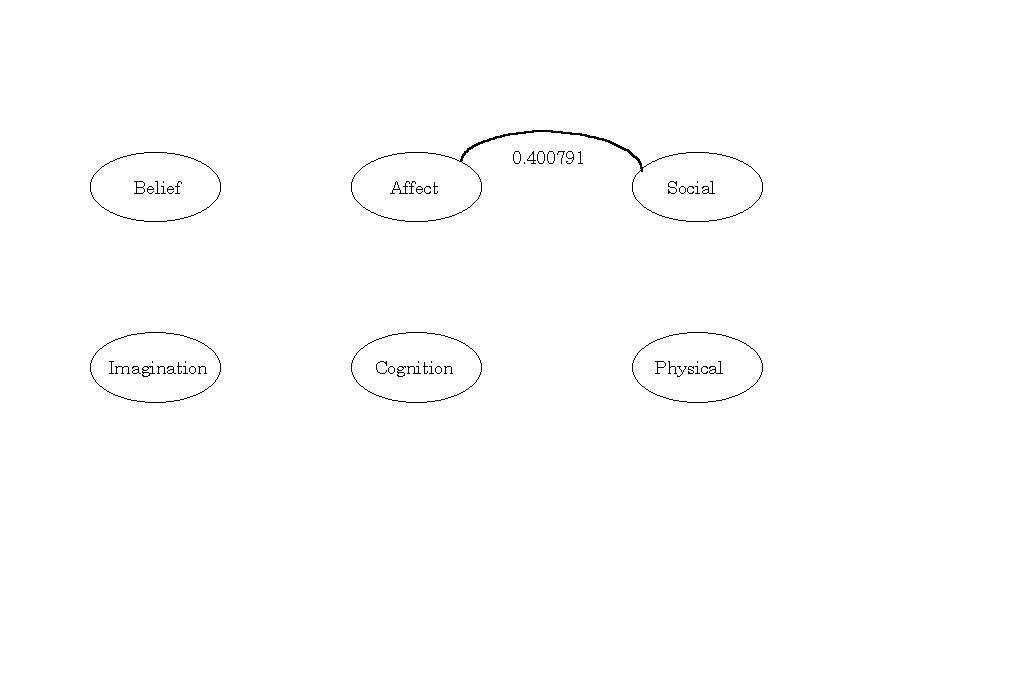
図14
AffectとSocialに相関関係があるパス図
表16 各モデルの適合度指標
| モデル |
GFI |
AGFI |
χ二乗値 |
自由度 |
AIC |
HCN |
|
1, 図13 |
.6456 |
.6092 |
1507.7891 |
819 |
-130.2109 |
71 |
|
2, 図14 |
.6462 |
.6123 |
1501.1313 |
824 |
-146.8687 |
72 |
表17 各モデル間のχ二乗値の差
| モデル比較 |
χ二乗値 |
|
1 vs 2 |
6.6570 |
表18 各モデル間のχ二乗値と自由度の比
| モデル |
χ二乗値と自由度との比 |
|
1,図13 |
1.8410 |
|
2,図14 |
1.8222 |
図13のモデルと図14のモデルのχ二乗値の差は
6.6570である(表17)。しかし、χ二乗分布は期待値と自由度が一致するため、χ二乗値は検定に利用するというよりも、むしろ自由度との比を求めておおよその適合度の程度として参照するにとどめるべきである(竹内, 1992)。そこで、各モデル間のχ二乗値と自由度との比を求めたのが表18である。このことから、図14のモデルは、図13のモデルよりも適合度がわずかではあるが有意に高いことが示された。複数のモデルを比較して、より優れたモデルを選ぶためには、χ二乗検定の他に
AIC(Akaike‘s Information Criterion)があり、これはモデルの説明力と安定性を統合した指標である。複数のモデルを比較して,AICの小さい方のモデルがより優れたモデルであるといえる。表16にもAICを示しているのだが、ここでも図14のモデルは、図13のモデルよりも優れているといえる。以上の評価から、図14のモデルが優れたモデルと認められた。しかし、χ二乗値と自由度の比が
1.8222とまだ大きく、このモデルがデータに適合しているかわからないため、今度はモデルの部分的評価を行い、再度モデルの修正を行うことにする。モデルの全体的な適合の評価を行い、モデルとデータとの適合が充分でない場合は、モデルを再構成し、よりよいモデルを探索しなくてはならない。モデルを再構成する場合は、母数や変数や方程式を別々に評価し、現時点までに構成されたモデルのどの部分に問題があるのかを診断することが有効である(竹内
, 1992)。ここでは、ラグランジュの乗数検定を行い、固定母数の中で自由母数に指定し直すべき母数があるか否かの検討を行った。この検定の結果、誤差項間の共分散(相関)を仮定して分析を行った方がよいという結果が出たため(表19)、モデルの中にそれを組み込み、さらにモデルを構成し、その結果を比較・評価した。すると、図14のモデルよりも、有意な数値のモデルを得ることができた(図15)。
表19 仮定した誤差項目間の共分散
| e1 e2 |
e1 e3 |
e 1 e4 |
e1 e5 |
e5 e25 |
e5 e28 |
e5 e31 |
e5 e8 |
e4 e8 |
e9 e40 |
|
e12e39 |
e15e19 |
e15e18 |
e16e18 |
e21e24 |
e22e10 |
e23e24 |
e25e26 |
e25e27 |
e25e28 |
|
e27e28 |
e29e34 |
e31e35 |
e31e14 |
e37e42 |
e37e41 |
e39e17 |
e40e23 |
e41e30 |
|